电影一区二区三区_亚洲激情二区_亚洲欧洲成人av每日更新_91超碰国产在线

<samp id="11111"></samp>

Calculus Integrals Math Sheet

An Engineers Quick Calculus Integrals Reference

Download PDF Download Image

$calculus integrals sheet$

Integrals Definition of an Integral Properties Common Integrals Integration by Subs. Integration by Parts Integration by Trig. Subs. Second Trig. Subs. Third Trig. Subs.

Integrals

Definition of an IntegralReturn to Top

The integral is a mathematical analysis applied to a function that results in the area bounded by the graph of the function, x axis, and limits of the integral. Integrals can be referred to as anti-derivatives, because the derivative of the integral of a function is equal to the function.

PropertiesReturn to Top

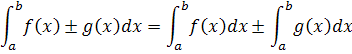
$the integral of the addition or subtraction of two functions$

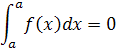
$the integral of a function where the two points of evaluation are the same$

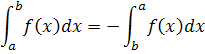
$the integral of a function where the two points of evaluation are swapped$

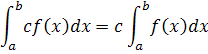
$the integral of a function multiplied by a constant$

Common IntegralsReturn to Top

$integral of a constant$

$integral of a variable raised to a power$

$integral of a x raised to -1 or 1 over x$

$integral of linear function raised to -1$

$integral of natural log function$

$integral of e to the x$

$integral of cosine function$

$integral of sine function$

$integral of secant squared function$

$integral of secant tangent function$

$integral of cosecant cotangent function$

$integral of cosecant squared function$

$integral of tangent function$

$integral of secant function$

$common integral with inverse tangent$

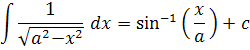
$common integral with inverse sine$

Integration by SubstitutionReturn to Top

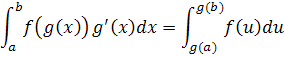
$integration by u substitution$

$integral by u substitution$

Integration by PartsReturn to Top

$integration by parts$

$integral by parts$

Integration by Trigonometric SubstitutionReturn to Top

Trigonometric identities can be use with integration substitution to simplify integrals. There are three common substitutions.

First Trigonometric SubstitutionReturn to Top

$first trignometric substitution$

To take advantage of the property

$integral by trig substitution$

Substitute

$substitute sin function$

$substitute cosine function for dx$

After substitution

$result of first trig substitution$

Second Trigonometric SubstitutionReturn to Top

$second trignometric substitution$

To take advantage of the property

$integral by trig substitution- secant squared$

Substitute

$integration substition for x - secant$

$trig substitution for dx$

After substitute

$result for second trig substitution$

Third Trigonometric SubstitutionReturn to Top

$third trigonometric substitution$

To take advantage of the property

$integral by trig substitution - tangent squared$

Substitute

$integration substitution for x - tangent$

$trig substitution for dx - secant squared$

After substitute

$result for third trig substitution$

主站蜘蛛池模板：邵武市| 青浦区| 桂阳县| 浦城县| 无棣县| 专栏| 禄丰县| 康定县| 安陆市| 南京市| 松潘县| 青神县| 石棉县| 务川| 依兰县| 大英县| 南投市| 旬阳县| 修水县| 鹰潭市| 封丘县| 紫阳县| 绥化市| 阜康市| 蓬莱市| 民丰县| 昌平区| 和田县| 大兴区| 石柱| 北票市| 永泰县| 彰化县| 重庆市| 迁安市| 潮州市| 霞浦县| 庆阳市| 黑河市| 左权县| 常山县|